Functions supporting mesh operations. More...

#include "EntityMap.h"
#include "Mesh.h"
#include "MeshTags.h"
#include "Topology.h"
#include "graphbuild.h"
#include "types.h"
#include <algorithm>
#include <array>
#include <basix/mdspan.hpp>
#include <boost/unordered/unordered_flat_map.hpp>
#include <cassert>
#include <concepts>
#include <cstdint>
#include <dolfinx/common/MPI.h>
#include <dolfinx/common/Timer.h>
#include <dolfinx/common/sort.h>
#include <dolfinx/graph/AdjacencyList.h>
#include <dolfinx/graph/ordering.h>
#include <dolfinx/graph/partition.h>
#include <format>
#include <functional>
#include <mpi.h>
#include <numeric>
#include <optional>
#include <ranges>
#include <span>
#include <stdexcept>
#include <variant>
#include <vector>

Include dependency graph for utils.h:

This graph shows which files directly or indirectly include this file:

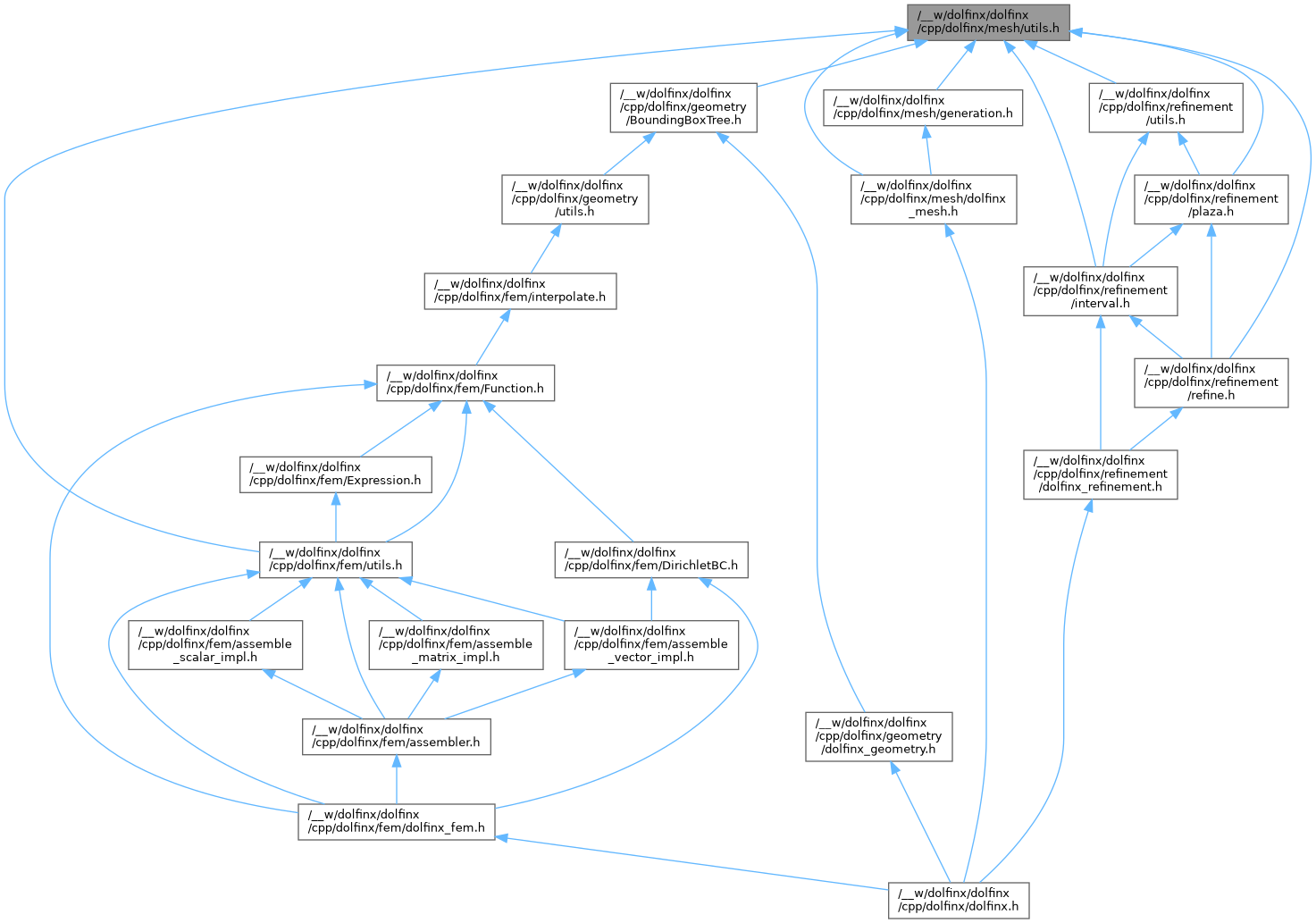
Go to the source code of this file.

Namespaces
namespace	dolfinx
	Top-level namespace.
namespace	dolfinx::fem
	Finite element method functionality.
namespace	dolfinx::mesh
	Mesh data structures and algorithms on meshes.

Concepts
concept	dolfinx::mesh::MarkerFn
	Requirements on function for geometry marking.

Typedefs
using	CellReorderFunction
	Function that reorders (locally) cells that are owned by this process. It takes the local mesh dual graph as an argument and returns a list whose ith entry is the new index of cell i.

Functions
template<typename T>
void	reorder_list (std::span< T > list, std::span< const std::int32_t > nodemap)
	Re-order the nodes of a fixed-degree adjacency list.
template<std::floating_point T>
std::tuple< std::vector< std::int32_t >, std::vector< T >, std::vector< std::int32_t > >	compute_vertex_coords_boundary (const mesh::Mesh< T > &mesh, int dim, std::span< const std::int32_t > facets)
	Compute the coordinates of 'vertices' for entities of a given dimension that are attached to specified facets.
std::vector< std::int32_t >	exterior_facet_indices (const Topology &topology, int facet_type_idx)
	Compute the indices of all exterior facets that are owned by the caller.
std::vector< std::int32_t >	exterior_facet_indices (const Topology &topology)
	Compute the indices of all exterior facets that are owned by the caller.
std::vector< std::int64_t >	reorder_cells (const CellReorderFunction &reorder_fn, std::optional< std::int32_t > max_facet_to_cell_links, const std::vector< CellType > &celltypes, const std::vector< fem::ElementDofLayout > &doflayouts, const std::vector< std::vector< int > > &ghost_owners, std::vector< std::vector< std::int64_t > > &cells, std::vector< std::span< std::int64_t > > &cells_v, std::vector< std::vector< std::int64_t > > &original_idx, int num_threads)
	Find a mesh's process boundary vertices, reordering cells for locality as a side effect.
std::vector< std::int64_t >	extract_topology (CellType cell_type, const fem::ElementDofLayout &layout, std::span< const std::int64_t > cells)
	Extract topology from cell data, i.e. extract cell vertices.
bool	is_vertex_dof_layout (CellType cell_type, const fem::ElementDofLayout &layout)
	Check if ::extract_topology is the identity operation for a dof layout, i.e. the cell 'nodes' are exactly the cell vertices, in vertex order ('P1 geometry').
template<std::floating_point T>
std::vector< T >	h (const Mesh< T > &mesh, std::span< const std::int32_t > entities, int dim)
	Compute greatest distance between any two vertices of the mesh entities (h).
template<std::floating_point T>
std::vector< T >	cell_normals (const Mesh< T > &mesh, int dim, std::span< const std::int32_t > entities)
	Compute normal to given cell (viewed as embedded in 3D).
template<std::floating_point T>
std::vector< T >	compute_midpoints (const Mesh< T > &mesh, int dim, std::span< const std::int32_t > entities)
	Compute the midpoints for mesh entities of a given dimension.
template<std::floating_point T>
std::pair< std::vector< T >, std::array< std::size_t, 2 > >	compute_vertex_coords (const mesh::Mesh< T > &mesh)
	The coordinates for all 'vertices' in the mesh.
template<std::floating_point T, MarkerFn< T > U>
std::vector< std::int32_t >	locate_entities (const Mesh< T > &mesh, int dim, U marker, int entity_type_idx)
	Compute indices of all mesh entities that evaluate to true for the provided geometric marking function.
template<std::floating_point T, MarkerFn< T > U>
std::vector< std::int32_t >	locate_entities (const Mesh< T > &mesh, int dim, U marker)
	Compute indices of all mesh entities that evaluate to true for the provided geometric marking function.
template<std::floating_point T, MarkerFn< T > U>
std::vector< std::int32_t >	locate_entities_boundary (const Mesh< T > &mesh, int dim, U marker)
	Compute indices of all mesh entities that are attached to an owned boundary facet and evaluate to true for the provided geometric marking function.
template<std::floating_point T>
std::pair< std::vector< std::int32_t >, std::array< std::size_t, 2 > >	entities_to_geometry (const Mesh< T > &mesh, int dim, std::span< const std::int32_t > entities, bool permute=false)
	Compute the geometry degrees of freedom associated with the closure of a given set of cell entities.
std::vector< std::int32_t >	compute_incident_entities (const Topology &topology, std::span< const std::int32_t > entities, int d0, int d1)
	Compute incident entities.
template<std::floating_point T>
std::vector< double >	compute_cell_centroids (MPI_Comm comm, std::span< const int > num_vertices_per_cell, const std::vector< std::span< const std::int64_t > > &cells, MPI_Comm commg, std::span< const T > x, int gdim)
	Compute the centroid of each cell from its vertex positions.
template<std::floating_point T>
std::tuple< std::vector< std::vector< std::int64_t > >, std::vector< std::vector< std::int64_t > >, std::vector< std::vector< int > > >	partition_cells (MPI_Comm comm, MPI_Comm commt, const std::vector< std::span< const std::int64_t > > &cells, const std::vector< CellType > &celltypes, const std::vector< fem::ElementDofLayout > &doflayouts, bool p1_geometry, const graph::Partitioner &partitioner, bool ghosting, std::optional< std::int32_t > max_facet_to_cell_links, int num_threads, MPI_Comm commg, std::span< const T > x, std::array< std::size_t, 2 > xshape)
	Partition cells across ranks of comm, or, if partitioner does not hold a callable function, assign each cell (which stays on its current rank) a globally unique index.
template<typename U>
Mesh< typename std::remove_reference_t< typename U::value_type > >	create_mesh (MPI_Comm comm, MPI_Comm commt, std::vector< std::span< const std::int64_t > > cells, const std::vector< fem::CoordinateElement< typename std::remove_reference_t< typename U::value_type > > > &elements, MPI_Comm commg, const U &x, std::array< std::size_t, 2 > xshape, const graph::Partitioner &partitioner, GhostMode ghost_mode, std::optional< std::int32_t > max_facet_to_cell_links, int num_threads, const CellReorderFunction &reorder_fn=graph::reorder_rcm)
	Create a distributed mesh::Mesh from mesh data and using the provided graph partitioning function for determining the parallel distribution of the mesh.
template<typename U>
Mesh< typename std::remove_reference_t< typename U::value_type > >	create_mesh (MPI_Comm comm, MPI_Comm commt, std::span< const std::int64_t > cells, const fem::CoordinateElement< typename std::remove_reference_t< typename U::value_type > > &element, MPI_Comm commg, const U &x, std::array< std::size_t, 2 > xshape, const graph::Partitioner &partitioner, GhostMode ghost_mode, std::optional< std::int32_t > max_facet_to_cell_links, int num_threads, const CellReorderFunction &reorder_fn=graph::reorder_rcm)
	Create a distributed mesh with a single cell type from mesh data and using a provided graph partitioning function for determining the parallel distribution of the mesh.
template<typename U>
Mesh< typename std::remove_reference_t< typename U::value_type > >	create_mesh (MPI_Comm comm, std::span< const std::int64_t > cells, const fem::CoordinateElement< std::remove_reference_t< typename U::value_type > > &elements, const U &x, std::array< std::size_t, 2 > xshape, GhostMode ghost_mode, std::optional< std::int32_t > max_facet_to_cell_links=2)
	Create a distributed mesh from mesh data using the default graph partitioner to determine the parallel distribution of the mesh.
template<std::floating_point T>
std::pair< Geometry< T >, std::vector< int32_t > >	create_subgeometry (const Mesh< T > &mesh, int dim, std::span< const std::int32_t > subentity_to_entity)
	Create a sub-geometry from a mesh and a subset of mesh entities to be included.
template<std::floating_point T>
std::tuple< Mesh< T >, EntityMap, EntityMap, std::vector< std::int32_t > >	create_submesh (const Mesh< T > &mesh, int dim, std::span< const std::int32_t > entities)
	Create a new mesh consisting of a subset of entities in a mesh.
template<typename T>
MeshTags< T >	transfer_meshtags_to_submesh (const MeshTags< T > &tags, std::shared_ptr< const dolfinx::mesh::Topology > submesh_topology, const EntityMap &vertex_map, const EntityMap &cell_map)
	Transfer a meshtags object from a parent to a submesh.

Detailed Description

Functions supporting mesh operations.

Function Documentation

◆ compute_cell_centroids()

template<std::floating_point T>

std::vector< double > compute_cell_centroids	(	MPI_Comm	comm,
		std::span< const int >	num_vertices_per_cell,
		const std::vector< std::span< const std::int64_t > > &	cells,
		MPI_Comm	commg,
		std::span< const T >	x,
		int	gdim )

Compute the centroid of each cell from its vertex positions.

Note: The returned centroids are always double, regardless of T, for the same reason as graph::geom_partition_fn: partition quality is insensitive to position precision.

Template Parameters

T	Scalar type of x.

Parameters

[in]	comm	Communicator that cells is distributed across.
[in]	num_vertices_per_cell	Number of vertices per cell, one entry per cell type of cells.
[in]	cells	Cells of each cell type, using global vertex indices (no higher-order 'nodes'). cells[i] is a flattened row-major array of shape (num_cells_i, num_vertices_per_cell[i]) for cell type i, where num_cells_i is however many cells of that type are on this rank.
[in]	commg	Communicator that x is distributed across.
[in]	x	Geometry ('node') coordinates, row-major with gdim columns, distributed over commg. Rows are addressed by the global vertex indices used in cells; only the rows for vertices referenced by cells on this rank are gathered from commg.
[in]	gdim	Number of coordinate components per node.

Returns: Cell centroids, row-major with gdim columns, one row per cell, with the cells of each cell type concatenated in the order they appear in cells.

◆ compute_vertex_coords()

template<std::floating_point T>

std::pair< std::vector< T >, std::array< std::size_t, 2 > > compute_vertex_coords ( const mesh::Mesh< T > & mesh )

The coordinates for all 'vertices' in the mesh.

Parameters

[in] mesh Mesh to compute the vertex coordinates for.

Returns: The vertex coordinates. The shape is (3, num_vertices) and the jth column hold the coordinates of vertex j.

◆ compute_vertex_coords_boundary()

template<std::floating_point T>

std::tuple< std::vector< std::int32_t >, std::vector< T >, std::vector< std::int32_t > > compute_vertex_coords_boundary	(	const mesh::Mesh< T > &	mesh,
		int	dim,
		std::span< const std::int32_t >	facets )

Compute the coordinates of 'vertices' for entities of a given dimension that are attached to specified facets.

Precondition: The provided facets must be on the boundary of the mesh.

Parameters

[in]	mesh	Mesh to compute the vertex coordinates for.
[in]	dim	Topological dimension of the entities.
[in]	facets	List of facets (must be on the mesh boundary).

Returns: (0) Entities attached to the boundary facets (sorted), (1) vertex coordinates (shape is (3, num_vertices)) and (2) map from vertex in the full mesh to the position in the vertex coordinates array (set to -1 if vertex in full mesh is not in the coordinate array).

◆ partition_cells()

template<std::floating_point T>

std::tuple< std::vector< std::vector< std::int64_t > >, std::vector< std::vector< std::int64_t > >, std::vector< std::vector< int > > > partition_cells	(	MPI_Comm	comm,
		MPI_Comm	commt,
		const std::vector< std::span< const std::int64_t > > &	cells,
		const std::vector< CellType > &	celltypes,
		const std::vector< fem::ElementDofLayout > &	doflayouts,
		bool	p1_geometry,
		const graph::Partitioner &	partitioner,
		bool	ghosting,
		std::optional< std::int32_t >	max_facet_to_cell_links,
		int	num_threads,
		MPI_Comm	commg,
		std::span< const T >	x,
		std::array< std::size_t, 2 >	xshape )

Partition cells across ranks of comm, or, if partitioner does not hold a callable function, assign each cell (which stays on its current rank) a globally unique index.

Template Parameters

T	Scalar type of x.

Parameters

[in]	comm	Communicator to distribute cells on.
[in]	commt	Communicator that cells is distributed on. Must be MPI_COMM_NULL on ranks that should not participate in computing the partition.
[in]	cells	Cells, grouped by cell type, as for ::create_mesh.
[in]	celltypes	Cell type, one entry per entry of cells.
[in]	doflayouts	Element dof layout, one entry per entry of cells.
[in]	p1_geometry	True if every layout in doflayouts is a vertex-only dof layout, so that a cell's 'nodes' are already exactly its vertices and extracting the topology is unnecessary.
[in]	partitioner	Partitioner, as for ::create_mesh, together with the node weights it is called with (one entry per cell in cells, flattened across cell types in the same order as cells; if std::nullopt, cells are treated as having equal weight). Used only if partitioner.fn holds a graph::partition_fn or a graph::hybrid_partition_fn.
[in]	ghosting	Flag to enable ghosting of the output cell distribution. Passed on to partitioner if it holds a graph::partition_fn or a graph::hybrid_partition_fn; has no effect if it holds a graph::geom_partition_fn, which can never ghost.
[in]	max_facet_to_cell_links	Bound on the number of cells a facet must be connected to for it to be considered matched (not on boundary for non-branching meshes). Used to build the mesh dual graph if partitioner holds a graph::partition_fn or a graph::hybrid_partition_fn; has no effect if it holds a graph::geom_partition_fn, which never needs the dual graph.
[in]	num_threads	Number of threads to use when building the mesh dual graph. Must be >= 1. Used only if partitioner holds a graph::partition_fn or a graph::hybrid_partition_fn.
[in]	commg	Communicator that x is distributed on. Used only if partitioner holds a graph::geom_partition_fn or a graph::hybrid_partition_fn.
[in]	x	Geometry ('node') coordinates. Used only if partitioner holds a graph::geom_partition_fn or a graph::hybrid_partition_fn.
[in]	xshape	Shape of x.

Returns

Cells assigned to this rank, by cell type, with all 'nodes' (not just vertices) and, if ghosted, any ghost cells appended.
The original global index of each cell in (1).
The owning rank of the ghost cells (the trailing entries) in (1).

◆ reorder_cells()

std::vector< std::int64_t > reorder_cells	(	const CellReorderFunction &	reorder_fn,
		std::optional< std::int32_t >	max_facet_to_cell_links,
		const std::vector< CellType > &	celltypes,
		const std::vector< fem::ElementDofLayout > &	doflayouts,
		const std::vector< std::vector< int > > &	ghost_owners,
		std::vector< std::vector< std::int64_t > > &	cells,
		std::vector< std::span< std::int64_t > > &	cells_v,
		std::vector< std::vector< std::int64_t > > &	original_idx,
		int	num_threads )

Find a mesh's process boundary vertices, reordering cells for locality as a side effect.

Logically this function only finds the vertices that may be shared with another process (from the facets unmatched by another local cell), which requires building the local dual graph. Since that is the same graph a cell reorder (e.g. for cache locality) is computed from, this function also applies reorder_fn to it and reorders cells, cells_v and original_idx in place, to avoid building the graph twice. reorder_fn is therefore required even though it plays no part in finding boundary vertices – it is bundled in because the two computations share the same dual graph.

Parameters

[in]	reorder_fn	Cell reorder function, applied to the local dual graph built internally.
[in]	max_facet_to_cell_links	Maximum number of cells a facet can be connected to.
[in]	celltypes	List of celltypes in mesh.
[in]	doflayouts	List of DOF layouts in mesh.
[in]	ghost_owners	List of ghost owner per cell per celltype.
[in,out]	cells	List of cells per celltype. Reordered during the call.
[in,out]	cells_v	List of vertices (no higher order nodes) of cell per celltype. Reordered during the call. cells_v[i] may alias cells[i] ('P1 geometry'), in which case it is reordered once only.
[in,out]	original_idx	Contains the permutation applied to the cells per celltype.
[in]	num_threads	Number of threads to use when building the local dual graph. Must be >= 1.

Returns: Boundary vertices (for all cell types).

◆ reorder_list()

template<typename T>

void reorder_list	(	std::span< T >	list,
		std::span< const std::int32_t >	nodemap )

Re-order the nodes of a fixed-degree adjacency list.

Parameters

[in,out]	list	Fixed-degree adjacency list stored row-major. Degree is equal to list.size() / nodemap.size().
[in]	nodemap	Map from old to new index, i.e. for an old index i the new index is nodemap[i].

Namespaces

Concepts

Typedefs

Functions

Detailed Description

Function Documentation

◆ compute_cell_centroids()

◆ compute_vertex_coords()

◆ compute_vertex_coords_boundary()

◆ partition_cells()

◆ reorder_cells()

◆ reorder_list()